- Today
- Total
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 정렬알고리즘
- programmer
- 다트
- swift split
- 알고리즘
- coding test
- dart
- 스위프트
- 디자인 패턴
- 프로그래머스 레벨2
- 정렬
- Design Pattern
- 코딩테스트
- 프로그래머스
- swift 알고리즘
- Algorithm
- swift 코딩테스트
- 감성에세이
- datastructure
- 디자인패턴
- swift
- 프로그래머스 swift
- 자료구조
- sort
- 정렬 알고리즘
- 스위프트디자인패턴
- 코테
- rxswift
- 프로그래머스 level1
- programmers
Bill Kim's Life...
[Algorithm] Big O Notation(빅 오 표기법) : 대표적인 점근 표기법, 알고리즘 공간 및 시간 복잡도 등에서 활용 본문
[Algorithm] Big O Notation(빅 오 표기법) : 대표적인 점근 표기법, 알고리즘 공간 및 시간 복잡도 등에서 활용
billnjoyce 2020. 6. 24. 14:47알고리즘에서의 점근표기법 및 Big O Notation(빅 오 표기법)에 대하여 살펴봅니다.
#. 구독 대상
- 컴퓨터 및 소프트웨어 공학과 관련자
- 소프트웨어 관련 종사자
- 기타 컴퓨터 공학에 관심이 있으신 분
- 알고리즘의 개념을 잡고 싶으신 분
- 기타 소프트웨어 개발과 지식에 관심이 있으신 모든 분들
점근 표기법(Asymptotic Notation)
컴퓨터 과학에서 알고리즘은 어떠한 문제를 최대한 빠르고 효율적으로 처리하기 위하여 사용합니다.
그러한 알고리즘에 대한 성능과 효율성을 측정하기 위해서 점근 표기법(Asymptotic Notation)이라는 것을 사용합니다.
점근 표기법에는 대표적으로 대문자 O 표기법, 대문자 오메가(Ω) 표기법, 대문자 세타(Θ) 표기법, 소문자 o 표기법, 소문자 오메가(ω) 표기법 다섯 종류가 있습니다.
하지만 우리가 실제로 많이 사용하는 방식은 대문자 O 표기법인 Big O 표기법을 많이 사용합니다.
Big-Ω notation
빅-오메가라고 읽으며 점근적 하한선을 의미합니다. (Asymptotic lower bound)
해당 알고리즘이 아무리 빨라도 기존 비교하는 함수와 같거나 혹은 좋지 않다는 뜻입니다.
정의 : Ω(g(n)) = { f(n) | 충분히 큰 n에 관해서 f(n)>= c*g(n)인 양의 "상수" c가 존재한다 }
예를 들어 2*n^2에 대해서는 Ω(n) 으로 표기할 수 있습니다.

Big O Notation
빅-오라고 부르며 점근적 상한선을 의미합니다. (Asymptotic upper bound)
즉 해당 알고리즘이 아무리 나빠도 기존 비교하는 함수와 같거나 혹은 좋다는 뜻입니다.
Big O 표기법이 알고리즘의 속도 및 공간 복잡도에서 대부분 객관적 지표로서 활용되는 표기법입니다.
정의 : O(g(n)) = { f(n) | 충분히 큰 n에 관해서 f(n)<= c*g(n)인 양의 "상수" c가 존재한다 }
f(n) = 5n^3 - n^2 는 빅오 표기법으로 하면 O(n^3)이 됩니다.

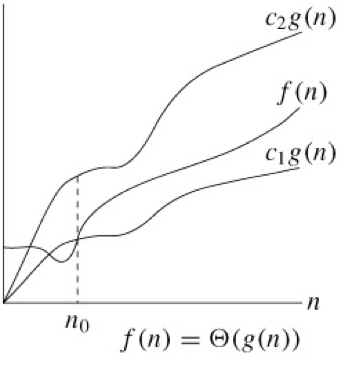
Big Θ-notation
빅-세타라고 부르는 말로서 점근적 상한과 하한의 교집합을 의미합니다. (Asymptotic tighter bound)
해당 알고리즘이 아무리 나쁘거나 좋더라도 기존의 비교하는 함수의 범위 안에 존재한다는 뜻입니다.
정의 : Θ(g(n)) = { Big O and Big Omega}
예를 들면 n^2+ 3*n+ 1023는 Θ(n^2)로 표기됩니다.
시간복잡도(Time Complexity)
시간복잡도(Time Complexity)는 어떤 문제를 해결하는데 걸리는 시간과 입력의 함수관계를 의미합니다.
알고리즘의 효율성에서 가장 중요한 평가 지표로 활용할 수 있습니다.
그럼 Big O 표기법으로 표기할 경우의 시간 복잡도의 종류를 한번 살펴보겠습니다.
Constant time : O(1)
상수 시간으로서 Big O 표기법으로 O(1)으로 표기되는 시간입니다.
스택에서 데이터를 넣고 빼고 할 경우 해당 시간이 소요됩니다.
데이터가 많아도 항상 같은 시간이 소요되는 경우를 말합니다.
가장 시간복잡도가 좋다고(빠르다) 할 수 있겠습니다.
Logarithmic time : O(logn)
로그 시간으로서 Big O 표기법으로 O(logn)으로 표기되는 시간입니다.
로그 함수처럼 데이터가 증가하여도 증가율이 많아질수록 적어지는 속도를 말합니다.
보통 이진 트리의 탐색에서 해당 시간을 갖습니다.
참고로 Big O 표기법에서의 로그의 밑수는 통상적으로 2(log2)로 간주합니다.
Linear time : O(n)
선형 시간으로서 Big O 표기법으로 O(n)으로 표기되는 시간입니다.
입력되는 데이터의 수만큼 계속 시간이 증가하는 경우를 말합니다.
배열이나 링크드 리스트에서 탐색할 경우 해당 시간이 소요됩니다.
Linearithmic time : O(n logn)
선형 로그 시간으로서 Big O 표기법으로 O(n logn)으로 표기되는 시간입니다.
선형 시간보다는 약간 느리다고 보면 되겠습니다.
데이터가 많아질 수록 완만하게 계속 늘어나는 모양을 취합니다.
보편적으로 사용되는 정렬 알고리즘에서 해당 시간을 보여주는데 퀵, 병합, 힙 정렬 등이 해상 시간을 가집니다.
Quadratic time : O(n^2)
다항 시간으로서 Big O 표기법으로 O(n^2)으로 표기되는 시간입니다.
입력되는 데이터의 4배(제곱)의 시간이 걸리는 것을 말합니다.
따라서 그리 효율적인 속도라고 볼 수 없습니다.
이중 루프문, 삽입 정렬, 선택 정렬, 버블 정렬 등이 이에 해당합니다.
Cubic time : O(n^3)
마찬가지로 다항 시간으로서 Big O 표기법으로 O(n^3)으로 표기되는 시간입니다.
O(n^2) 마찬가지로 입력되는 데이터가 많아질 수록 기하급수적으로 늘어납니다. O(n^3)은 데이터 수의 3제곱(8배) 수만큼 늘어납니다.
마찬가지로 효율적인 속도라고 볼 수 없습니다. 삼중 루프문 등이 이에 해당합니다.
Exponential time : O(2^n)
지수 시간으로서 Big O 표기법으로 O(2^n)으로 표기되는 시간입니다.
최악의 시간 복잡도를 나타내며 실제로 해당 시간이 걸리는 데이터가 많을 경우 알고리즘은 사용 여부를 고려해볼 필요가 있습니다.
피보나치 수열의 경우 해당 시간을 가질 수 있습니다.
Factorial time : O(n!)
계승 시간으로서 Big O 표기법으로 O(n!)으로 표기되는 시간입니다.
사실상 일정 수 이상은 일반적인 컴퓨터로 계산할 수 없는 시간을 가집니다.
이산 수학 등에서 팩토리얼의 경우 해당 시간을 가집니다.
위에서 살펴본 시간 복잡도에 대해서 그래프 다이어그램으로 살펴보면 아래와 같습니다.

이상으로 지금까지 점근표기법 및 Big O Notation(빅 오 표기법)에 대하여 설명하였습니다.
오늘은 간만에 비가 내리고 있습니다. 잠시 더위를 식혀주는 비라서 반가운 하루입니다.
그럼 남은 오후도 행복한 시간되세요. ^^
감사합니다.
[참고 자료(References)]
[1] 빅 오 표기법(Big O notation) : https://johngrib.github.io/wiki/big-O-notation/
[2] 점근 표기법 : https://ko.wikipedia.org/wiki/점근_표기법
[3] 빅오 표기법 (big-O notation) 이란 : https://noahlogs.tistory.com/27
[4] [Complexity Analysis] Time Complexity and Big-O Notation : https://velog.io/@shaqok/Complexity-Analysis-Time-Complexity-and-Big-O-Notation
[5] big-O notation : https://velog.io/@hanrimjo/big-O-notation
[6] Learning Big O Notation with Swift : https://medium.com/swift-algorithms-data-structures/learn-big-o-notation-with-swift-4ab83195859e
[7] Complexity and Big-O Notation In Swift : https://medium.com/journey-of-one-thousand-apps/complexity-and-big-o-notation-in-swift-478a67ba20e7
[8] A Beginner's Guide to Big O in Swift : https://learnappmaking.com/big-o-notation-swift/
[9] An introduction to Big O in Swift : https://www.donnywals.com/an-introduction-to-big-o-in-swift/
[10] Big O Notation : https://dennis-xlc.gitbooks.io/swift-algorithms-data-structures/chapter1.html
[11] [Algorithm] Time Complexity : https://velog.io/@junyong92/TIL-Time-Complexity
[12] [알고리즘] 점근적 표기법 : https://satisfactoryplace.tistory.com/70
'CS(컴퓨터 과학) > Algorithm' 카테고리의 다른 글
| [Algorithm] Sorting Comparison : 정렬 알고리즘 종류와 특징, 그리고 효율성 (0) | 2020.06.24 |
|---|---|
| [Algorithm] Counting Sort(계수 정렬) : 각 숫자의 카운팅 배열을 활용하여 정렬하는 알고리즘 (0) | 2020.06.19 |
| [Algorithm] Radix Sort(기수 정렬) : 자릿수를 비교하여 정렬하는 알고리즘 (0) | 2020.06.19 |
| [Algorithm] Shell Sort(쉘 정렬) : 삽입 정렬을 보완한 정렬 알고리즘 (0) | 2020.06.19 |
| [Algorithm] Heap Sort(힙 정렬) : 힙 트리를 활용한 정렬 알고리즘 (0) | 2020.06.19 |




