- Today
- Total
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 디자인 패턴
- swift 알고리즘
- dart
- 프로그래머스
- 프로그래머스 swift
- swift 코딩테스트
- 디자인패턴
- 다트
- 정렬 알고리즘
- coding test
- 스위프트디자인패턴
- 자료구조
- Algorithm
- programmers
- 코딩테스트
- 정렬알고리즘
- 프로그래머스 level1
- rxswift
- swift split
- datastructure
- 감성에세이
- 코테
- programmer
- Design Pattern
- swift
- sort
- 정렬
- 스위프트
- 프로그래머스 레벨2
- 알고리즘
Bill Kim's Life...
[자료구조] BFS(너비 우선 탐색) : 그래프, 최단/최소 경로를 구해보자 본문
자료구조의 한 종류인 BFS(너비 우선 탐색)에 대해서 살펴봅니다.
#. 구독 대상
- 컴퓨터 및 소프트웨어 공학과 관련자
- 자료구조 개념을 잡고 싶으신 분
- 소프트웨어 관련 종사자
- 기타 컴퓨터 공학에 관심이 있으신 분
- 기타 소프트웨어 개발과 지식에 관심이 있으신 모든 분들
- Swift 언어를 활용하여 자료구조를 공부해보고 싶으신 분들
BFS(너비 우선 탐색)
BFS(Bredth-First Search)란 그래프(Graph)에서 노드를 탐색하기 위한 하나의 알고리즘 방법으로서 너비 우선 검색이라는 방식입니다.
BFS를 사용하여 최단 및 최소 경로를 구할 수 있습니다.
BFS는 큐를 통하여 최소한의 비용이 필요한 경로를 구합니다.
모든 곳을 탐색하는 것보다 최소 비용이 우선일 경우 본 알고리즘이 적합합니다.
기본 동작
BFS의 기본적인 알고리즘 흐름은 다음과 같습니다.
1. 시작할 노드를 Queue에 넣는다.(Enqueue)
2. Queue에서 노드를 하나 꺼낸다.(Dequeue)
3. Dequeue한 노드와 인접한 노드가 있는지 확인한다.
4. Dequeue한 노드를 출력한다.
5. Dequeue한 노드와 인접한 노드를 Queue에 Enqueue한다.
이미 방문한 노드는 Enqueue 하지 않는다.
6. 2번 부터 5번까지의 과정을 Queue가 비워질때까지 반복한다.
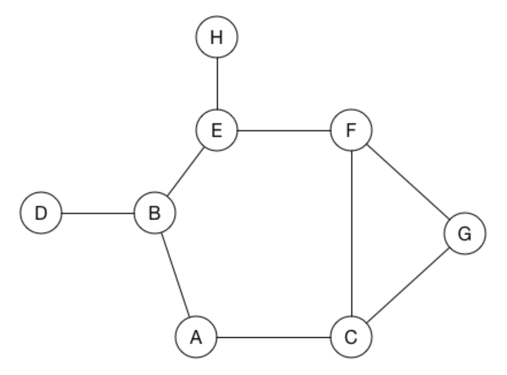
탐색 과정 : 무방향 그래프
앞서 설명한 알고리즘을 아래의 예시를 통해서 살펴보겠습니다.
BFS 알고리즘을 통하여 A 노드에서 시작한 경로에 대한 과정을 살펴보면 다음과 같습니다.
(1)
(2)

(3)
(4)

(5)

(6)

(7)

(8)
(9)
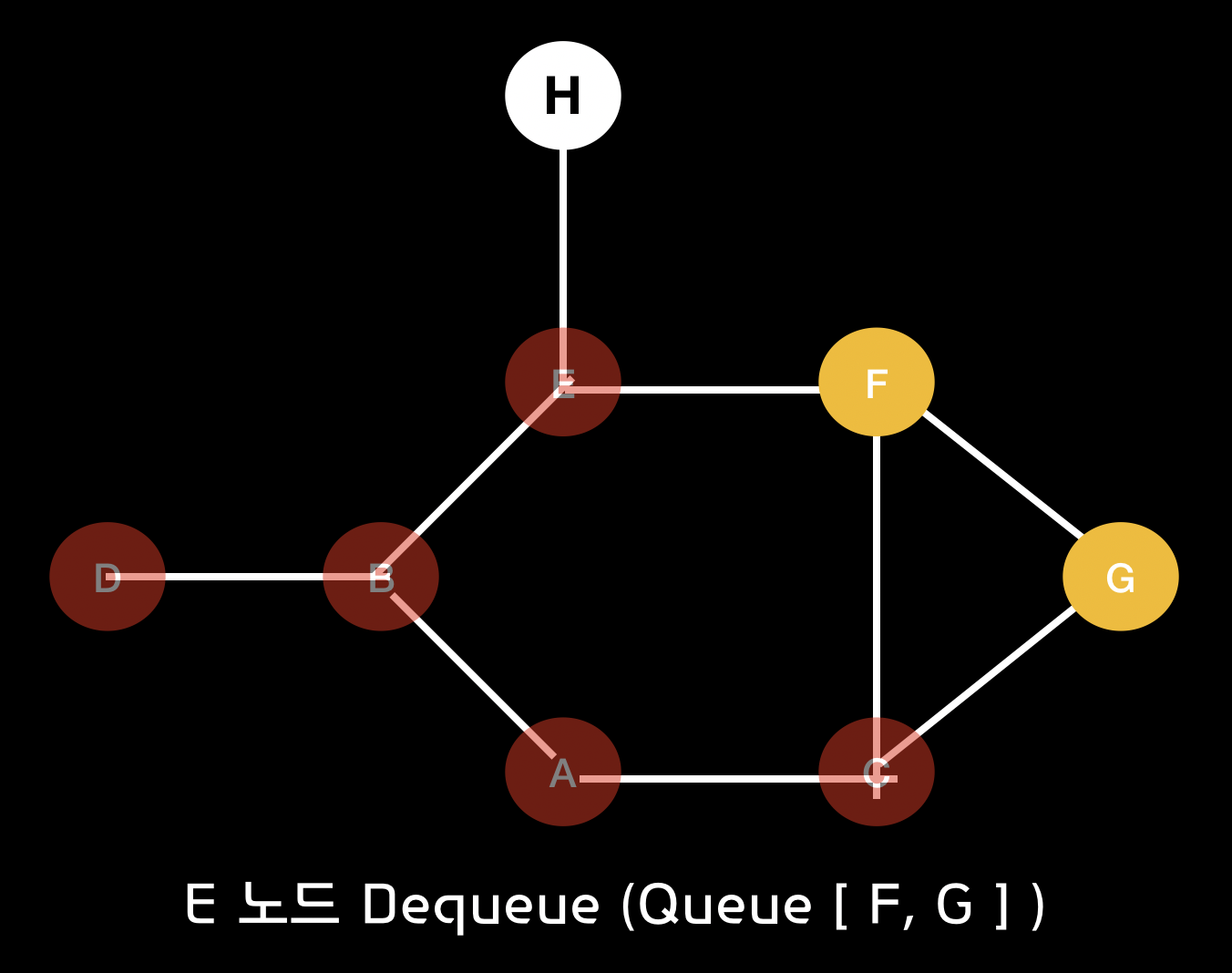
(10)
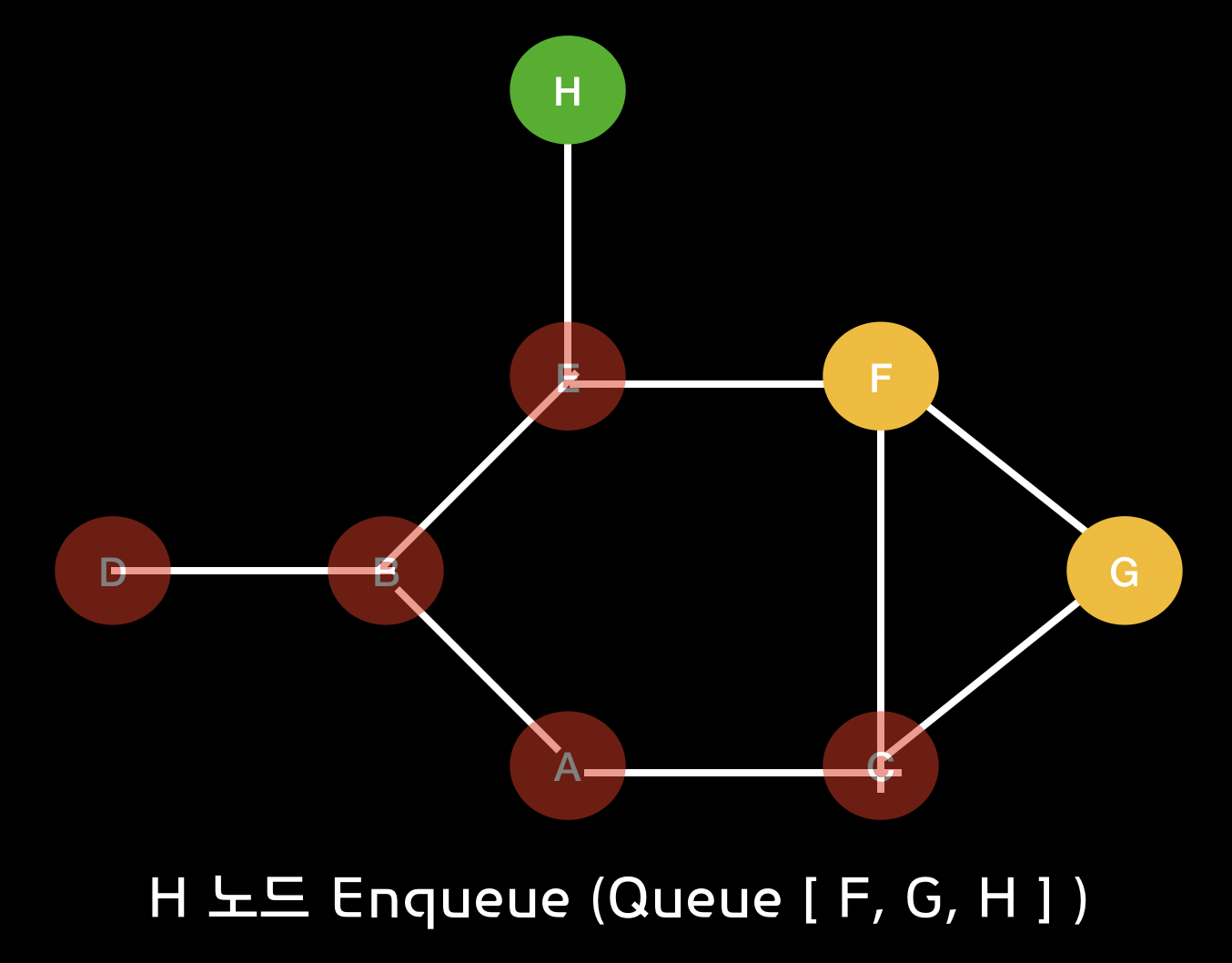
(11)

(12)

(13)
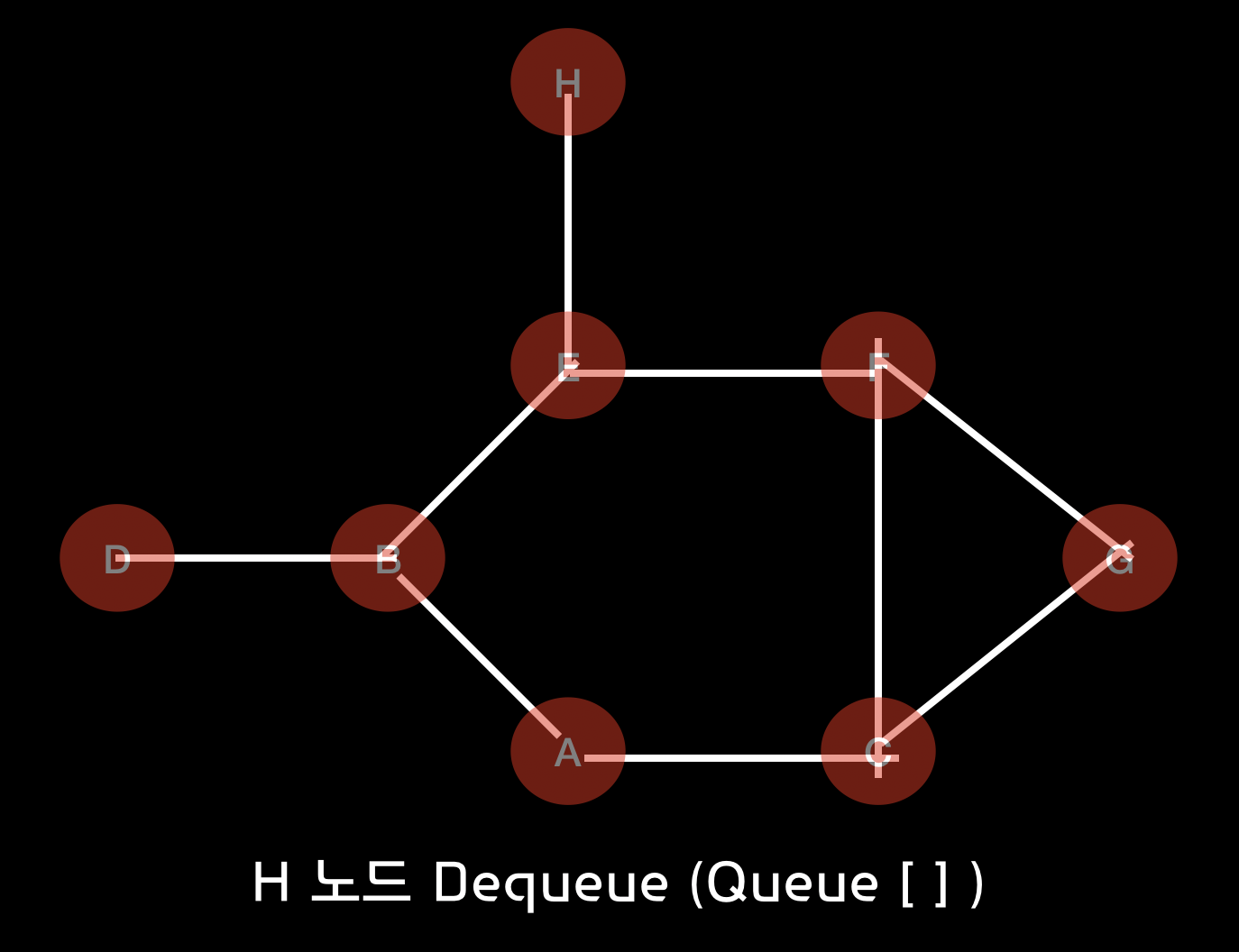
최종 경로를 살펴보면 아래와 같습니다.
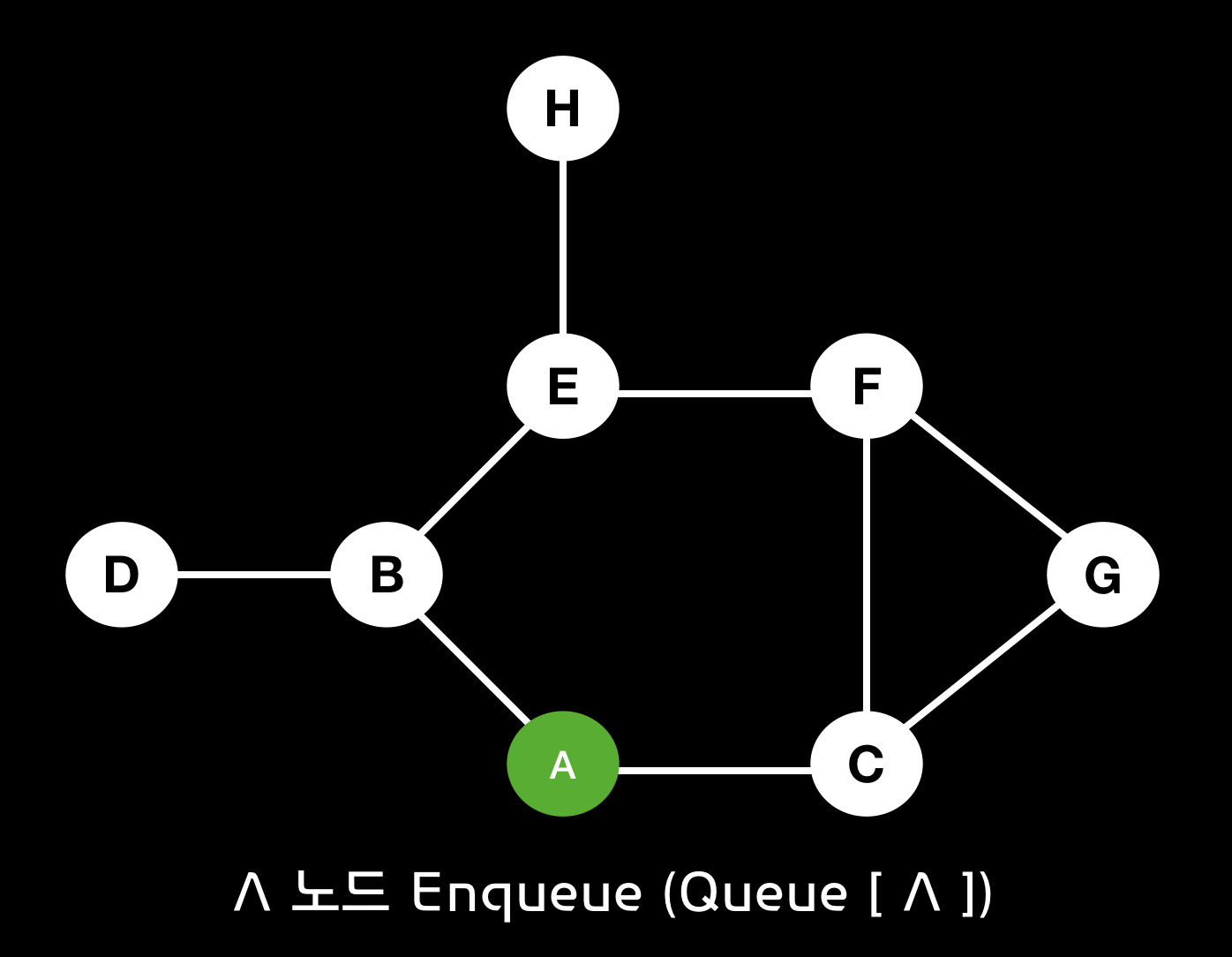
Enqueue(+) : a - Queue [ a ]
Dequeue(-) : a - Queue [ ] => a
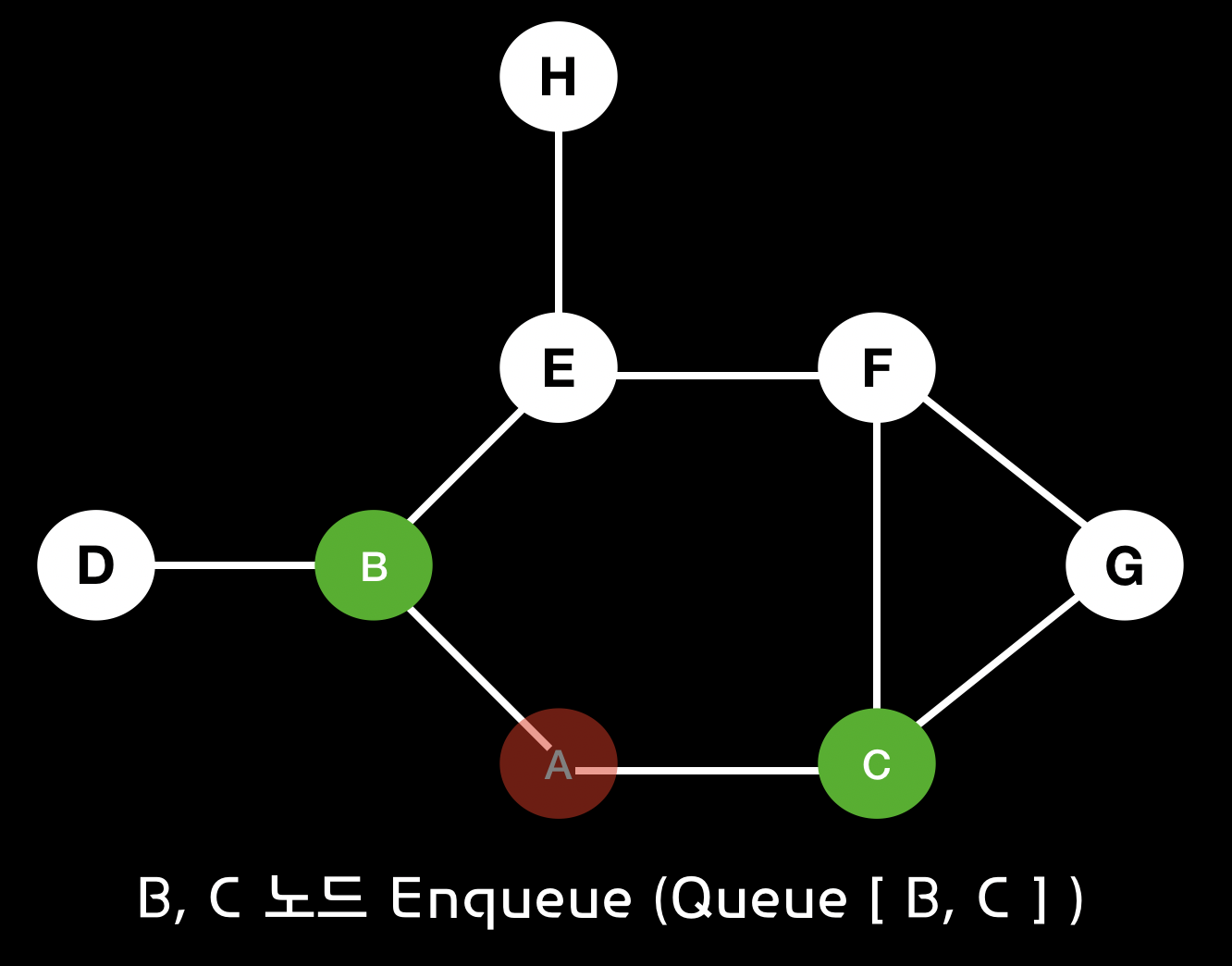
Enqueue(+) : b - Queue [ b ]
Enqueue(+) : c - Queue [ b, c ]
Dequeue(-) : b - Queue [ c ] => a, b
Enqueue(+) : d - Queue [ c, d ]
Enqueue(+) : e - Queue [ c, d, e ]
Dequeue(-) : c - Queue [ d, e ] => a, b, c
Enqueue(+) : f - Queue [ d, e, f ]
Enqueue(+) : g - Queue [ d, e, f, g ]
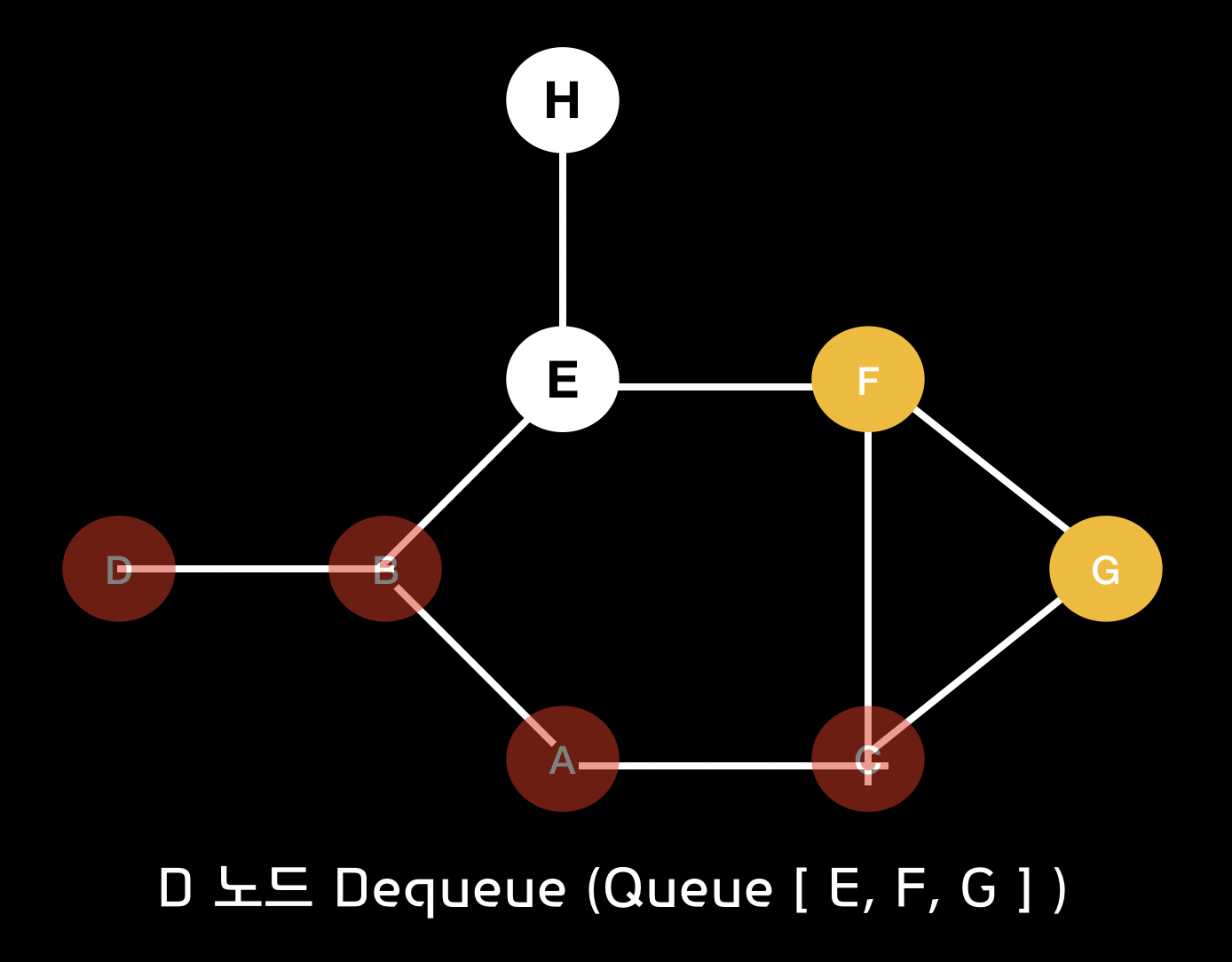
Dequeue(-) : d - Queue [ e, f, g ] => a, b, c, d
Dequeue(-) : e - Queue [ f, g ] => a, b, c, d, e
Enqueue(+) : h - Queue [ f, g, h ]
Dequeue(-) : f - Queue [ g, h ] => a, b, c, d, e, f
Dequeue(-) : g - Queue [ h ] => a, b, c, d, e, f, g
Dequeue(-) : h - Queue [ ] => a, b, c, d, e, f, g, h
최종 경로 : [“a", "b", "c", "d", "e", "f", "g", "h"]
방향 그래프에서의 최단 경로 탐색
이번에는 방향 그래프에서의 모든 경로 탐색에 대한 또다른 예제를 살펴보겠습니다.
만약 1번 노드에서 출발하여 각 노드들의 최단 루트는 아래와 같습니다.
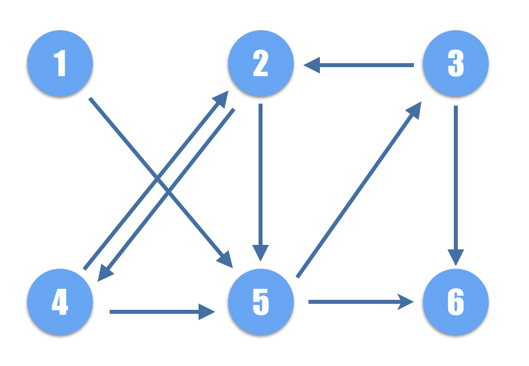
1번 노드를 루트로 두는 방향 그래프에서, BFS를 이용해 MST(Minimum Spanning Tree)를 만드는 과정을 거치면 다음과 같은 과정이 진행됩니다.
(1)
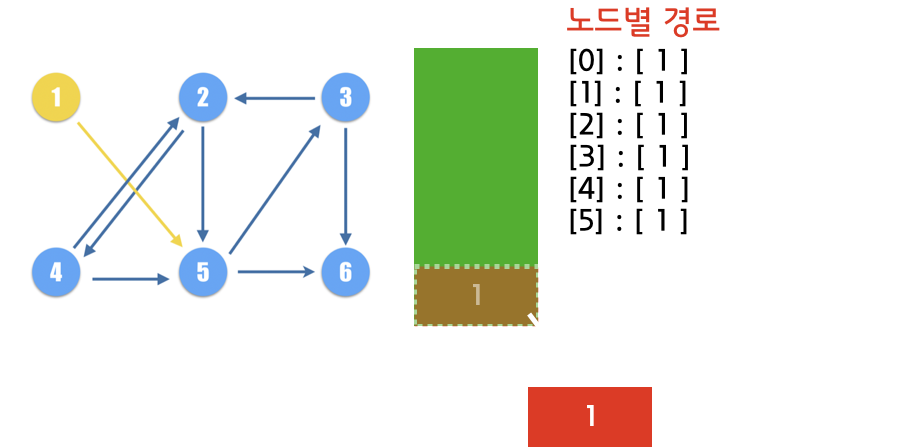
(2)
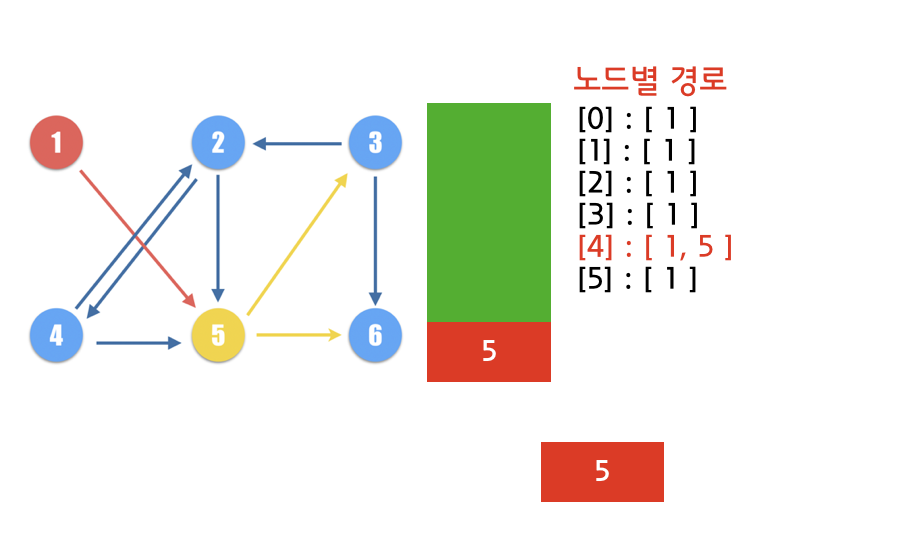
(3)

(4)

(5)
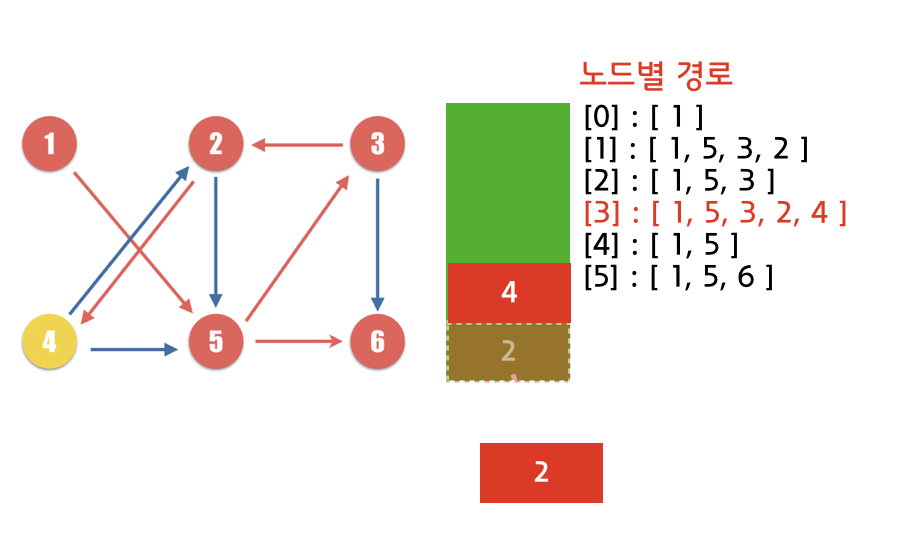
(6)

(7)

만약 1번 노드에서 출발하여 각 노드들의 최단 루트를 살펴보면 아래와 같습니다.
1 -> 5 -> 3 -> 2
1 -> 5 -> 3
1 -> 5 -> 3 -> 2 -> 4
1 -> 5
1 -> 5 -> 6
Implementation
Swift를 활용하여 가장 기본적인 위에서 살펴본 2개의 예제를 직접 구현해보겠습니다. 우선 필요한 객체와 메소드는 아래와 같습니다.
필요한 객체
- 정점(Vertex) 객체
- 간선(Edge) 객체
- breadthFirstSearch : BFS(너비 우선 탐색)를 실행하는 함수
NodeGraph 클래스
public class NodeGraph : CustomStringConvertible, Equatable {
public var neighbors: [EdgeGraph]
public private(set) var label: String
public var distance: Int?
public var visited: Bool
public init(_ label: String) {
self.label = label
neighbors = []
visited = false
}
public var description: String {
if let distance = distance {
return "Node(label: \(label), distance: \(distance))"
}
return "Node(label: \(label), distance: infinity)"
}
public var hasDistance: Bool {
return distance != nil
}
public func remove(_ edge: EdgeGraph) {
neighbors.remove(at: neighbors.index { $0 === edge }!)
}
static public func == (_ lhs: NodeGraph, rhs: NodeGraph) -> Bool {
return lhs.label == rhs.label && lhs.neighbors == rhs.neighbors
}
}
EdgeGraph 클래스
public class EdgeGraph : Equatable {
public var neighbor: NodeGraph
public init(_ neighbor: NodeGraph) {
self.neighbor = neighbor
}
static public func == (_ lhs: EdgeGraph, rhs: EdgeGraph) -> Bool {
return lhs.neighbor == rhs.neighbor
}
}
NodeGraphPath 클래스
class NodeGraphPath<T>
{
let value: T
var edges = [EdgeGraphPath<T>]()
var visited = false
init(value: T) {
self.value = value
}
func appendEdgeTo(_ node: NodeGraphPath<T>) {
let edge = EdgeGraphPath<T>(from: self, to: node)
self.edges.append(edge)
}
}
EdgeGraphPath 클래스
class EdgeGraphPath<T> {
weak var source: NodeGraphPath<T>?
let destination: NodeGraphPath<T>
init(from source: NodeGraphPath<T>, to destination: NodeGraphPath<T>) {
self.source = source
self.destination = destination
}
}
BFS 함수
func breadthFirstSearch(_ graph: Graph, source: NodeGraph) -> [String] {
let queue = Queue<NodeGraph>()
// 최초 시작 위치를 Queue 에 담습니다.
queue.enqueue(source)
print("Enqueue(+) : \(source.label)")
var nodesExplored = [source.label]
// 최초 노드를 방문한 것으로 표시합니다.
source.visited = true
while let current = queue.dequeue() {
print("Dequeue(-) : \(current.label)")
for edge in current.neighbors {
let neighborNode = edge.neighbor
if !neighborNode.visited {
queue.enqueue(neighborNode)
print("Enqueue(+) : \(neighborNode.label)")
neighborNode.visited = true
nodesExplored.append(neighborNode.label)
}
}
}
return nodesExplored
}
func breadthFirstSearch(n: Int, edges: [(Int, Int)]) -> [Any] {
let nodes = (0..<n).map({ NodeGraphPath<Int>(value: $0 + 1) })
for (from, to) in edges {
nodes[from - 1].appendEdgeTo(nodes[to - 1])
}
var shortest = Array(repeating: [1], count: n)
let queue = Queue<NodeGraphPath<Int>>()
// 시작 노드를 큐에 삽입 및 방문 상태 체크
queue.enqueue(nodes[0])
nodes[0].visited = true
// 큐에서 최상단 노드를 하나씩 빼면서 큐가 비어 있을 때까지 반복
while let node = queue.dequeue() {
for edge in node.edges {
let dest = edge.destination
// 현재 대상 노드를 큐에 삽입 및 방문 상태 체크
guard dest.visited == false else { continue }
queue.enqueue(dest)
dest.visited = true
// 현재 노드에 대한 총 이동 경로 노드를 저장
shortest[dest.value - 1] = shortest[node.value - 1] + [dest.value]
}
}
return shortest
}
사용 예시
// 무방향 그래프 관련 사용 예시
let graph = Graph()
let nodeA = graph.addNode("a")
let nodeB = graph.addNode("b")
let nodeC = graph.addNode("c")
let nodeD = graph.addNode("d")
let nodeE = graph.addNode("e")
let nodeF = graph.addNode("f")
let nodeG = graph.addNode("g")
let nodeH = graph.addNode("h")
graph.addEdge(nodeA, neighbor: nodeB)
graph.addEdge(nodeA, neighbor: nodeC)
graph.addEdge(nodeB, neighbor: nodeD)
graph.addEdge(nodeB, neighbor: nodeE)
graph.addEdge(nodeC, neighbor: nodeF)
graph.addEdge(nodeC, neighbor: nodeG)
graph.addEdge(nodeE, neighbor: nodeH)
graph.addEdge(nodeE, neighbor: nodeF)
graph.addEdge(nodeF, neighbor: nodeG)
// Enqueue(+) : a - Queue [ a ]
//
// Dequeue(-) : a - Queue [ ] => a
// Enqueue(+) : b - Queue [ b ]
// Enqueue(+) : c - Queue [ b, c ]
// Dequeue(-) : b - Queue [ c ] => a, b
// Enqueue(+) : d - Queue [ c, d ]
// Enqueue(+) : e - Queue [ c, d, e ]
// Dequeue(-) : c - Queue [ d, e ] => a, b, c
// Enqueue(+) : f - Queue [ d, e, f ]
// Enqueue(+) : g - Queue [ d, e, f, g ]
// Dequeue(-) : d - Queue [ e, f, g ] => a, b, c, d
// Dequeue(-) : e - Queue [ f, g ] => a, b, c, d, e
// Enqueue(+) : h - Queue [ f, g, h ]
// Dequeue(-) : f - Queue [ g, h ] => a, b, c, d, e, f
// Dequeue(-) : g - Queue [ h ] => a, b, c, d, e, f, g
// Dequeue(-) : h - Queue [ ] => a, b, c, d, e, f, g, h
print(nodesExplored)
// ["a", "b", "c", "d", "e", "f", "g", "h"]
// 방향 그래프 관련 사용 예시
print(breadthFirstSearch(n: 6, edges: [(1,5), (2,4), (2,5), (3,2), (3,6), (4,2), (4,5), (5,3), (5,6)]))
// [[1]
// [1, 5, 3, 2],
// [1, 5, 3],
// [1, 5, 3, 2, 4],
// [1, 5],
// [1, 5, 6] ]
이상으로 자료구조의 BFS(너비 우선 탐색)에 대해서 살펴보았습니다.
감사합니다.
www.slideshare.net/BillKim8/swift-data-structure-graphbfs-234889410
[Swift] Data Structure - Graph(BFS)
Swift를 활용하여 자료구조에 대해서 설명하는 강의 자료입니다. 본 강의는 Graph(BFS)에 대해서 구체적으로 예제와 함께 설명을 하는 강의 자료입니다.
www.slideshare.net
[참고 자료(References)]
[1] Swift로 그래프 탐색 알고리즘을 실전 문제에 적용해보기 - BFS 편 : https://wlaxhrl.tistory.com/89
[2] DFS (Depth-First Search) BFS (Breadth-First Search) 개념 : https://hucet.tistory.com/83
[3] [알고리즘] DFS & DFS : https://hyesunzzang.tistory.com/186
[4] 너비 우선 탐색 : https://ko.wikipedia.org/wiki/너비_우선_탐색
[5] [Data Structure] 그래프 순회, 탐색(DFS) - 자료 구조 : https://palpit.tistory.com/898
[6] DFS (Depth-First Search) BFS (Breadth-First Search) 개념 : https://hucet.tistory.com/83
[7] Understanding Depth & Breadth-First Search in Swift : https://medium.com/swift-algorithms-data-structures/understanding-depth-breadth-first-search-in-swift-90573fd63a36
[8] Breadth first search : https://www.programiz.com/dsa/graph-bfs
[9] [알고리즘] BFS & DFS : https://hyesunzzang.tistory.com/186
[10] 자료구조 :: 그래프(2) "탐색, 깊이우선, 너비우선 탐색” : http://egloos.zum.com/printf/v/755736
'CS(컴퓨터 과학) > Data Structure' 카테고리의 다른 글
| [자료구조] DFS(깊이 우선 탐색) : 그래프, 모든 경로를 구해보자 (0) | 2020.06.12 |
|---|---|
| [자료구조] Graph(그래프) : 비선형(Non-Linear) 자료구조, 최단거리/최소거리 알고리즘 (0) | 2020.06.12 |
| [자료구조] Binary Tree(이진 트리) : 자식이 2개인 트리, 검색이 빠름 (0) | 2020.06.12 |
| [자료구조] Tree(트리) : 계층적 자료구조 (0) | 2020.06.12 |
| [자료구조] Heap(힙) : 이진 트리를 배열로 표시, 최대값/최소값 빨리 찾기 (0) | 2020.06.12 |





